고정 헤더 영역
상세 컨텐츠
본문
2주차에는 IK 구현을 위한 준비를 진행하였다.
1. Camera 객체 구현
Camera 객체는 키보드와 마우스 입력으로 위치와 각도를 조절하는 객체로, CameraPos, CameraUp, CameraFront 벡터를 통해 렌더링에 필요한 view Matrix를 반환한다.
2. Model 렌더링
저번 주에 학습한 DX11 지식을 활용하여 Model 렌더링을 구현했다. Model은 여러 개의 Mesh 객체와 Texture 객체들로 구성되며, Model 정보는 Assimp 라이브러리를 통해, Texture 데이터는 DirectXTex 라이브러리를 통해 로딩했다.
3. Skeleton Animation 정보 로딩
Skeleton Animation 정보 역시 Assimp 라이브러리를 이용하여 로딩했다. 정보를 저장하는 클래스 및 구조체는 다음과 같다:
struct Bone {
std::string name;
int parentIndex = -1;
std::vector<int> children;
XMMATRIX offsetMatrix;
};
class Skeleton {
public:
std::vector<Bone> bones;
std::unordered_map<std::string, int> nameToIndex;
int rootBoneIdx;
int GetBoneIndex(const std::string& name) const;
};
struct PositionKeyframe {
double time;
XMFLOAT3 position;
};
struct RotationKeyframe {
double time;
XMFLOAT4 rotation;
};
struct ScaleKeyframe {
double time;
XMFLOAT3 scale;
};
struct BoneTrack {
std::string boneName;
std::vector<PositionKeyframe> positionKeys;
std::vector<RotationKeyframe> rotationKeys;
std::vector<ScaleKeyframe> scaleKeys;
};
struct AnimationClip {
std::string name;
double duration; // 총 Tick 수
double ticksPerSecond; // 1초당 몇 Tick인지
std::unordered_map<std::string, BoneTrack> boneTracks;
BoneTrack* GetTrack(const std::string& boneName);
};
- Bone: 부모 및 자식 Bone 정보, offsetMatrix(기본 Bone의 변환 행렬의 역행렬)를 저장.
- Skeleton: 전체 Bone들의 정보를 저장.
- PositionKeyframe, RotationKeyframe, ScaleKeyframe: 각 키프레임 별 Position, Rotation, Scale 정보를 시간에 대응하여 저장.
- BoneTrack: 애니메이션 클립에서 Bone 1개의 시간에 따른 Position, Rotation, Scale의 변화 저장
- AnimationClip: 하나의 애니메이션 클립의 정보를 저장하고 있으며, Bone 마다의 애니메이션 정보를 BoneTrack 객체를 통해 저장
4. Skeleton Animation Skinning 적용
Skinning은 Vertex가 여러 Bone의 영향을 받아 움직이도록 하는 기법이다. Assimp에서 Vertex마다 영향을 주는 상위 4개의 Bone과 가중치를 추출하여 저장하고, 이 값을 정규화해 사용했다.
Vertex Shader에 Skinning을 적용하기 위해 현재 프레임에서 Bone 변환 행렬을 미리 구하는데, 이를 Pose 객체에 저장한다:
struct Pose {
std::vector<XMMATRIX> local;
std::vector<XMMATRIX> world;
std::vector<XMMATRIX> finalMatrix;
int count;
void Initialize(size_t boneCount);
void ApplyHierarchy(const Skeleton& skeleton);
};- local: Bone의 Local 변환
- world: 부모의 Local 변환까지 반영한 변환
- finalMatrix: offsetMatrix까지 적용한 최종 변환
각 Matrix는 Bone의 개수만큼 존재한다. 이를 Vertex Shader 상수 버퍼에 load한 뒤 skinning을 위해 사용한다.
5. 애니메이션 재생 및 블렌딩
애니메이션 블렌딩은 두 가지로 나누어 구현했다:
- 같은 애니메이션의 시간에 따른 블렌딩
- 애니메이션 정보를 시간마다 준비를 하는 경우 데이터가 너무 많이 필요하기 때문에, keyframe이라는 특정 시간의 데이터들만 준비해 놓는다. 만약 현재 시간에 준비되어있는 애니메이션 정보가 없는경우 이전 keyframe의 정보와 다음 keyframe의 정보를 보간하여 새로운 애니메이션을 만들어 사용한다. 보간은 keyframe들의 시간과 현재 시간을 통해 가중치를 정한 후 진행한다.
- 애니메이션 간 블렌딩
- 만약 Walk 상태에서 Idle 상태로 바로 전환되는 경우 모든 Bone이 순간이동하여 부자연스러워 보일 수 있다. 따라서 애니메이션간의 전환에도 블렌딩이 필요하다. 만약 A -> B 로 전환을 해야하는 경우 Blending Alpha라는 값을 준비하여 0.0f 부터 1.0f 까지 증가시킨다.
여기서 Blending Alpha는 A와 B를 보간하는 가중치이며 0.0f인 경우 이전 애니메이션인 A를 100% 사용하는 것이고 1.0f인 경우 다음 애니메이션인 B를 100% 사용하는 것이다. Blending Alpha가 1.0f가 된 경우 애니메이션 전환이 완료된 것이라 볼 수 있다.
- 만약 Walk 상태에서 Idle 상태로 바로 전환되는 경우 모든 Bone이 순간이동하여 부자연스러워 보일 수 있다. 따라서 애니메이션간의 전환에도 블렌딩이 필요하다. 만약 A -> B 로 전환을 해야하는 경우 Blending Alpha라는 값을 준비하여 0.0f 부터 1.0f 까지 증가시킨다.
6. Key 입력에 따른 애니메이션 전환 및 컨트롤
- 애니메이션 전환
- 애니메이션은 Idle과 Walk만 준비되어있는 상태이므로, 상태 전환도 Idle -> Walk와 Walk -> Idle 2가지가 가능하다. 화살표 4개 중 1개라도 눌린 상태라면 Walk, 아니면 Idle 상태로 전환된다.
- 캐릭터 속도 설정
- Walk 애니메이션은 제자리에서 걷는 애니메이션으로 움직이는 경우 모델 자체를 직접 속도를 줘야 한다. 화살표를 눌러 Walk 상태가 되면 화살표 방향으로 캐릭터가 움직이기 시작하고, 속도는 정해진 가속도를 기반으로 증가한다. 속도가 max 값에 다다르면 그 속도를 유지하며, Idle 상태로 전환되는경우 정해진 가속도에 맞게 속도가 감소한다.
- 캐릭터 방향 설정
- 캐릭터 진행 방향은 화살표 방향과 같지만 실제 캐릭터의 Front 방향은 입력된 화살표 방향을 목표로 서서히 변한다. 정해진 속도에 맞게 변하며 화살표 방향과 일치하게 되면 회전을 멈추게 된다.
7. 디버깅용 Skeleton Rendering 추가
디버깅을 위해 Bone과 Joint 렌더링을 추가하였다. Joint는 기존 관절의 위치에 구를 빨간색으로 그려넣었고, Bone은 부모 Joint와 자식 Joint 사이에 얇은 직사각형을 그려넣었다.
Bone을 렌더링 할때는 점 4개를 (0,0,0)에 넣고 Draw를 호출하였으며 점 2개는 Parent Joint위치로 나머지 2개는 Child Joint 위치로 변환 시킨 후, 두껍게 보일 수 있도록 각 Joint 위치에서 2개의 점을 서로 떨어뜨려 놓았다. 이때 떨어뜨리는 벡터는 Camera의 Front 벡터와 Parent Joint -> Child Joint 벡터를 cross한 방향으로 떨어뜨려 놓아서 카메라에서 늘 일정한 두께의 직사각형 본을 볼 수 있게 만들었다.
8. IK 적용 계획
IK 적용을 하기 위한 기본 준비를 마치고 FBIK 적용 전 Fook IK를 통한 경사로 걷기를 위한 계획을 짜보았다.
1. Physx를 이용한 Raycasting 도입
특정 Bone이 Target 근접했는지를 판단하기 위해 Raycasting이 필요하다. 이는 나중에 Ragdoll 도입시 사용할 Physx에 있는 기능이므로 Physx를 이용하기로 하였다.
2. Jacobian Matrix를 이용한 IK 적용
IK 적용을 위한 알고리즘에 4가지가 있었고 이를 다 공부해보았다.
다음 용어를 통해 설명할 것이기 때문에 이를 알고 들어가자.
Root : Root Bone
Bone(n) : Root로 부터 n번째 Bone
EndEffector : 원하는 곳으로 움직이고 싶은 Bone
Target : EndEffector가 목표로하는 위치
Triangulation IK (Two-Bone IK)
이 알고리즘은 제 2의 코사인 법칙을 이용한 알고리즘이다. 제 2의 코사인 법칙은 삼각형 3변의 길이를 아는 경우 각도를 알 수 있다는 법칙인데, 우리는 이를 이용하여 삼각형 3개의 변을 만들고 각도를 구할 것이다.
우선 root 부터 EndEffector까지 bone들을 target 방향으로 일자로 쭉 핀다. 이제 3개의 변을 구할 것이다. 첫번째 변은 root 부터 target까지의 거리이다. 두번째, 세번째 변은 쭉 펴놨던 Bone들을 하나의 Bone을 기준으로 나눈 것들이다.
기준으로 정한 Bone을 n번째 Bone이라고하면 제 2의 코사인 법칙을 통해 n번째 Bone의 각도를 구할 수 있게 되고 관절의 제약이 없는 경우 EndEffector가 Target에 갈 수 있게 된다.
위 방법은 2개의 Bone에서 효과적이지만 여러개의 Bone인 경우 부자연스러운 움직임이 나오는 경우가 많다.
CCD (Cyclic Coordinate Descent)
CCD는 EndEffector -> Root 방향으로 모든 Bone에 대해 각도 조절을 적용하는 것이다. EndEffector -> Root 순서대로 각도 조절하는 것을 EndEffector가 target에 근사하거나 정해놓은 반복횟수를 다 채울때까지 반복한다.
각 Bone들은 아래와 같은 과정을 통해 각도를 조절한다.
1) 현재 Bone -> EndEffector 벡터 구하기
2) 현재 Bone -> Target 벡터 구하기
3) 두 벡터의 각도 차이만큼 bone 각도 수정
위와 같이 각도 수정을 EndEffector -> Root 순서대로 Bone에 적용하다 보면 EndEffector가 Target에 근사하게 된다.
이 알고리즘은 단일 Chain 에 적용하기 좋은 아주 빠른 알고리즘이지만 각 관절의 회전이 독립적으로 이루어지므로, FBIK 적용에는 어울리지 않는다.
다음 블로그 글을 보면 참고가 될 것이다.
https://velog.io/@tjswodud/GE2022-6.-Heuristic-Inverse-Kinematics-Algorithms
[GE] 6. Heuristic Inverse Kinematics Algorithms
본 포스트는 2022년 1학기에 진행한 게임공학 수업 내용을 정리한 것임을 알려드립니다.FABRIK 등장 이전에 많이 쓰이던 방식.CCD는 articulated body의 interactive control을 수행하기에 좋은 heuristic 기술임.
velog.io
FABRIK (Forward and Backward Reaching IK)
CCD가 각도 조절을 통해 반복하여 결과에 수렴했다면 FABRIK은 위치 조절을 통해 결과에 수렴하는 방법이다.
CCD와 다르게 FABRIK은 두 단계를 반복하며 수렴에 도달한다.
(1) 첫번쨰 스테이지
첫번째 스테이지는 EndEffector -> Root 방향으로 진행된다. 시작하는 경우 우선 EndEffector를 Target에 위치시킨다. 이렇게 EndEffector가 이동하고 부모 Bone이 따라와야하는데 이때 이동한 EndEffector와 부모 Bone을 이은 선에서 기존 Bone 사이의 길이에 맞게 부모 Bone을 이동시킨다. 이것을 Root 까지 반복하면 첫번째 스테이지가 끝난다.
(2) 두번쨰 스테이지
두번째 스테이지는 Root를 기존 Root 자리에 옮기고 시작한다. 첫번째 스테이지에서 했던 것들을 Root -> EndEffector 방향으로 똑같이 진행해주면 된다.
두번쨰 스테이지까지 진행된 경우 CCD때와 마찬가지로 EndEffector가 target에 근접했거나 정해놓은 반복횟수에 다다른 경우까지 계속 반복해준다.
만약 IK Chain이 여러개인 경우 여러 개의 EndEffector들에서 첫번째 스테이지를 시작하는데, 이때는 chain이 합쳐지는 분기마다 분기가 되는 Bone의 위치를 평균값이나 가중치를 적용해서 정하면 된다.
FABRIK은 CCD보다 자연스러운 움직임이 가능하고 FBIK로 확장도 가능하며 연산이 가벼운 편이다. 그러나 위치 기반으로 움직이다 보니 늘 각도를 역산하여 구해야하고, 각도에 대한 제약 등을 적용하기가 쉽지 않다.
https://velog.io/@tjswodud/GE2022-6.-Heuristic-Inverse-Kinematics-Algorithms#2-triangulation-ik-2
Jacobian IK
Jacobian IK는 Jacobian Matrix를 이용해서 IK를 구현하는 것이다.
이 방법을 이해하려면 먼저 다변수 함수의 연쇄 법칙을 이해해야 한다.

다음과 같은 식이 있을때 θ1, θ2, ... θn 들이 t에대해 미분이 가능한 경우

아래와 같은 식으로 변환할 수 있다. 자세한 설명은 아래 블로그에서 볼 수 있다.
https://angeloyeo.github.io/2020/07/24/Jacobian.html
자코비안(Jacobian) 행렬의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
A = B(x) 이고 x = g(z) 인 경우 우리가 dA/dt를 구하기 위해 dA/dz * dz/dt를 알면 된다는 것인데 이를 말로 풀어보면 A에 대한 z의 변화율을 알고 t에 대한 z의 변화율을 알아서 결국 A에 대한 t의 변화율을 얻을 수 있는 것이다.
어쨋든 위 방법으로 아래와 같이 [시간에 대한 EndEffector -> Target의 위치 차이] = [Jacobian Matrix] * [시간에 대한 joint의 각도 변화]를 통해 우리는 모든 joint 들의 각도를 구하는 것이다.
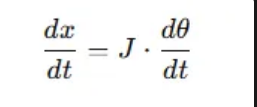
위와 같은 방법으로 현재 EndEffector와 Target사이의 거리와 Jacobian 행렬을 통해 EndEffector가 Target에 도달하기 위한 모든 joint의 각도 값을 근사하게 구할 수 있다. 이 과정에서 dx를 조금씩 적용하여 여러번 반복을 통해 결과에 수렴하도록 한다.
FABRIK vs Jacobian IK
FBIK까지 본다면 이 둘 중에 하나를 선택해야한다. 나는 둘 중에 Jacobian IK를 선택했고 이유는 다음과 같다.
1. FABRIK은 위치 기반이므로 각도가 필요할때마다 역산해야한다.
2. FABRIK은 FBIK에서 Chain을 추가할때마다 구조적으로 많이 변경해야한다.
3. FABRIK은 관절 제약을 걸거나 가중치를 적용하는 것이 Jacobian IK 보다 어렵다.
4. Jacobian IK는 무게중심을 고려하는 체인을 만들어 좀 더 현실적인 움직임이 가능하다.
물론 Jacobian IK가 연산이 너무 많다는 단점이 있지만 1개의 애니메이션만 보일 예정이기 떄문에 이는 최적화를 통해 처리할 예정이다.
Foot IK에서 포함할 Jacobian IK 기능
우선 FBIK를 구현하기 전에 Foot IK를 적용할 에정인데 Jacobian IK의 다음 기능들을 포함할 것이다.
1. Jacobian 계산
2. dθ 를 구하기 위한 방법 -> Pseudo-inverse (Moore-Penrose), Damped Least Squares (DLS) ...
3. Weight Matrix
4. 관절 제약 설정
3. Root Bone인 골반 위치 보정
Foot IK 적용 후 경사를 올라갈 경우 골반이 그대로 있으면 캐릭터가 경사를 오르지 못할 것이다. 디딤발을 기준으로 Root Bone인 골반의 y값을 보정해주면서 자연스러운 움직임을 구현해야 한다.
4. Phase 시스템 도입
디딤발이 바뀌는 경우, IK를 적용하는 경우, IK를 해제하는 경우 등을 맞추기 위해 Phase를 도입하여 타이밍을 계산할 예정이다.
5. 발 디딜 곳 예측 후 궤도 계산
기존 애니메이션만 적용하면 경사에 따라 보폭이 달라지거나 발의 궤적이 어색할 수 있다. 따라서 자연스러운 걸음을 구현하기 위해 앞으로 Ray를 발사해 다음 발 디딜 곳을 찾고 거기에 맞게 발의 궤적을 찾아 IK를 적용하여 발을 움직일 예정이다.
'Computer Graphics > Hiking' 카테고리의 다른 글
| Hiking: 6주차 Foot IK를 적용한 이동 구현 (0) | 2025.05.09 |
|---|---|
| Hiking: 5주차 하체 100% IK 적용 (0) | 2025.05.02 |
| Hiking: 4주차 Joint Clamping 적용 (0) | 2025.04.25 |
| Hiking: 3주차 Jacobian IK 적용 (1) | 2025.04.18 |
| Hiking: Procedural Animation을 활용한 등산 시뮬레이션 프로젝트 (0) | 2025.04.03 |




